ML) Multiple Regression
2022. 8. 29. 22:32ㆍML_DL/ML
다변수 선형회귀

RSS 식의 벡터화
RSS의 식과 벡터의 norm을 연관 지을 수 있다.
e =(e(1),...,e(n))
e(i) = y(i) - y(hat)(i)
를 이용하면,

이때, 벡터 y 와 predictor matrix X가 주어지면, 해당 식은 beta의 함수로 표현이 되어 지는 것이다.
추정모형의 결과로 Coefficient (beta_value) 를 구했을 때, 음수의 값을 갖거나 굉장히 작은 경우에는 해당 predictors는 다른 predictor와 독립적인 관계가 아닐 수 있다.
HOW TO UNDERSTAND ?
- response, predictor 관계 파악
- 어떤 변수가 중요한가?
- 모형이 얼마나 잘 적합 되었는가?
- 설명변수들의 값이 있을때, 예측된 반응변수값과 해당 예측값은 얼마나 정확한가?
Response , Predictor
추정모형의 분석에 앞서서, Response 와 Predictor를 F-statics를 통해 가설을 검정할 수 있다.
귀무가설 : Beta 값들은 모두 0 이다 ( 서로 관계가 없다.)
대립가설 : 적어도 하나의 Beta 값은 0이 아니다 (서로 관계가 있다.)
이를 F-statics를 통해 검정한다.

어떤 변수가 중요한가?
- 변수의 중요성에 앞서서 우리는 적합된 모형에 대해 성능을 확인할 수 있다.
즉, 우리가 어느 데이터에 대해서 선형회귀,트리,시계열 관련 모델 등 중에서 하나의 모델을 선택했을때, 그 모델이 얼마나 적합한지를 수치로 표현해준다.
(예: AIC, BIC, Mallow’s Cp, adjusted R-square)
다만 같은 비교군에서만 비교가 가능하고 , 어느 분석법이 좋은지에 대한 판명을 어렵다.
어떤 변수가 중요할까?
- All subset Selection
- Forward Selection
- Backward Selection
Forward Selection
- n 개의 변수들 (X)가 있을 때 먼저 변수를 하나만 사용한 모형을 적합한다.
- 이를 n번 진행하여, 가장 좋은 모형을 선택한다.
- 선택된 변수는 포함한 뒤 다시 (n-1)번의 진행을 통해서 가장 적합한 모형을 선택한다.
- 해당 행위를 반복한다. ( 변수를 더 추가 할지 말지의 척도는 뭘까? )
- 위에서 임의의 변수들을 선택한 모형의 적합성 판단은 위에 명시했던 AIC , BIC등을 이용한다.
Beta값 추정
import numpy as np
# scipy도 가능하지만, P-value, Statics value확인에 용이한 statsmodels 사용
import statsmodels.api as sm
# 관측치의 개수
N = 1000
# 정규분포를 이용해 데이터를 생성(N(0,1))
X = np.random.normal(loc = 0, scale = 1, size = (N,1))
# 절편(상수항)을 추가
X = sm.add_constant(X)
# 정규분포를 이용해 오차항을 생성(N(0,1) 분포)
epsilon = np.random.normal(loc = 0, scale = 1, size=(N,1))
# 실제 모형 : Y = 2 + 3X + epsilon
Y = X @ np.array([[2], [3]]) + epsilon
# 단순회귀모형
simple_reg = sm.OLS(Y,X).fit()
print(simple_reg.summary())
적합된 회귀계수 평균으로 Beta 값 확인하기
N = 1000
# 반복 횟수
repeat_num = 1000
beta = np.zeros((2, ))
for k in range(repeat_num):
# 정규분포 (N(0,1))
X = np.random.normal(loc =0, scale =1 ,size =(N,1))
# 절편(상수항) 추가
X = sm.add_constant(X)
epsilon = np.random.normal(loc =0, scale =1 ,size =(N,1))
Y = X @ np.array([[2], [3]]) + epsilon
simple_reg = sm.OLS(Y, X).fit()
beta += simple_reg.params
# 적합된 회귀 계수의 평균 계산
beta /= repeat_num
print(beta)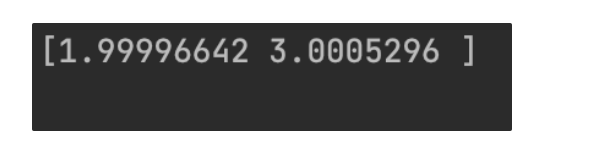
'ML_DL > ML' 카테고리의 다른 글
| ML) CrossValidation (0) | 2022.08.30 |
|---|---|
| ML) Metrics (0) | 2022.08.29 |
| ML) Logistic Regression (0) | 2022.08.29 |
| ML) Ridge Regression (0) | 2022.08.29 |
| ML) 선형회귀 ( Linear Regression ) (0) | 2022.08.25 |